Dieser Inhalt ist unter einer Creative Commons-Lizenz lizenziert.
Dieser Inhalt ist unter einer Creative Commons-Lizenz lizenziert.Datenabhängigkeitsanalyse als Teilaufgabe dynamischer Optimierung
Abstrakt:
Dieser Text beschäftigt sich mit einem Verfahren zur
Datenabhängigkeitsanalyse. Zu diesem Zweck werden einführend einige
allgemeine Grundlagen erläutert, welche im Verlauf des Textes an einem
Beispiel für einen konkreten Algorithmus beziehungsweise an einem
konkreten Programmblock vertieft werden.
1)
1)Hauptquelle und Bezug: Chambers, Pechtchanski,
Sarkar, Serrano, Srinivasan. Dependency Analysis for Java. IBM.
1. Einführung
1.1 Was ist Abhängigkeitsanalyse
Die „Datenabhängigkeitsanalyse“ ist ein Werkzeug, welches Daten über ein zugrunde liegendes Programmfragment liefert. Ein Programmfragment ist in der Regel eine Folge elementarer Anweisungen oder Zeilen von Programmcode, welche in eine Folge elementarer Anweisungen überführt werden können. Die durch eine Abhängigkeitsanalyse gewonnenen Daten können die Grundlage bilden für eine nachfolgende Optimierung des Programmfragments. Diese Optimierung könnte zum Beispiel eine Identifikation parallel ausführbarer Anweisungen sein, um eine beschleunigte Abarbeitung des Programmfragments auf Parallelrechnern zu ermöglichen. Eine konkrete Anwendung wären Verfahren wie „Instruction Reordering“, beziehungsweise „Instruction Scheduling“. Das Ergebnis einer Datenabhängigkeitsanalyse kann als „Datenabhängigkeitsgraph“ dargestellt werden. Ein Datenabhängigkeitsgraph besteht aus Knoten und Kanten.
Alle Knoten repräsentieren voneinander verschiedene elementare Anweisungen. Die Kanten repräsentieren jeweils eine „Datenabhängigkeit“. Jede Datenabhängigkeit stellt eine Beziehung zwischen zwei elementaren Anweisungen des Progammfragments dar. Je nachdem welche Art von Beziehung vorliegt, können die Kanten unterschiedlich beschriftet sein. Eine Anweisung heißt in diesem Dokument „elementar“, falls sie sich als Lese- oder Schreibzugriff auf maximal ein Datum auffassen lässt. Es gibt mehrere bekannte Verfahren eine Repräsentation eines Datenabhängigkeitsgraphen in sequentieller Form zu erzeugen und zu speichern. Eine bekannte Möglichkeiten Abhängigkeiten zwischen skalaren Variablen darzustellen, liefert zum Beispiel die SSA-Form (static single assignment form). Jedoch mit der Einschränkung, dass SSA keine referenz- und typsichere Repräsentation bietet.
1.2 Zielsetzung
Von einem Verfahren zur Datenabhängigkeitsanalyse wird erwartet, dass alle elementaren Anweisungen zwischen denen das Verfahren keine Abhängigkeitsbeziehung liefert, garantiert unabhängig im Sinne der Datenabhängigkeitsanalyse sind. Es ist ein Ziel eines solchen Verfahrens, möglichst exakte Ergebnisse zu liefern, ohne gegen die Forderung der Korrektheit zu verstossen. Ein Ergebnis ist umso exakter, je höher die Wahrscheinlichkeit ist, dass eine gefundene Abhängigkeitsbeziehung zwischen 2 elementaren Anweisungen auch zur Laufzeit des Programms Bestand hat. Dies ist deshalb von entscheidender Bedeutung, weil gilt: je exakter die Daten über enthaltene Abhängigkeiten in einem Programmfragment sind, umso bessere Ergebnisse können nachfolgende Optimierungsschritte liefern, welche diese Daten zur Grundlage nehmen.
Die Forderung nach Korrektheit ist trivialerweise erfüllt, wenn ein vollständig verbundener Abhängigkeitsgraph als Ergebnis geliefert wird. Das Verfahren hat also die Aufgabe zu versuchen, möglichst viele der Kanten des vollständig verbundenen Graphen auszuschliessen. Das Problem, eine perfekte Lösung für diese Aufgabenstellung zu finden lässt ist jedoch NP-vollständig. Jedes eingesetzte Verfahren liefert daher stets lediglich einen möglichst guten Kompromiss zwischen Geschwindigkeit und Exaktheit des Ergebnisses.
1.3 mathematische Sicht
Aus mathematischer Sicht definiert ein konkretes Verfahren zur Datenabhängigkeitsanalyse eine Äquivalenzrelation, welche eine Menge von elementaren Anweisungen in Äquivalenzklassen zerlegt. Alle Elemente der selben Äquivalenzklasse sind elementare Anweisungen, welche bezüglich eines bestimmten Datums voneinander abhängig sind. Für ein im Sinne der Datenabhängigkeitsanalyse völlig unabhängiges Programmfragment gilt, dass alle entstehenden Äquivalenzklassen einelementig sind.
Das heißt, der Datenabhängigkeitsgraph hat 0 Kanten, weil keine Abhängigkeiten vorhanden sind. Ein vollständig abhängiges Programmfragment besitzt dementsprechend genau 1 Äquivalenzklasse welche alle elementaren Anweisungen enthält. Der Datenabhängigkeitsgraph wäre in diesem Fall der vollständig verbundene Graph.
2. Beispiel
Datenabhängigkeitsanalyse erfordert mindestens 3 Arbeitsschritte.
1) Auffinden der Daten auf welche sich die
nachfolgende Analyse bezieht.
2) Umwandeln der Befehlszeilen des Programmfragments in elementare Lese- und
Schreibzugriffe auf diesen Daten.
3) Analyse des so vorbereiteten Programmfragments. Eventuell
4) Aufbereitung der gewonnenen Daten, zum Beispiel in Form einer
Darstellung als Datenabhängigkeitsgraph.
Im folgenden Abschnitt des Dokumentes werden diese Arbeitsschritte exemplarisch an einem konkreten Programmbeispiel nachvollzogen, um einen Eindruck vom Ablauf eines Verfahrens in der Praxis zu vermitteln.
2.1 Programmfragment
Folgendes Programmfragment in Java-Syntax wird dem in diesem Abschnitt beschriebenen Beispiel zugrunde gelegt. Es wird vorausgesetzt, dass alle enthaltenen Vorkommen von Variablen korrekt definiert und initialisiert wurden.
0 a:=b+c;
1 if (a==1) {
2 b:=b+1; };
3 RefTy d := new RefTy(a,b);
4 RefTy e := new RefTy(b,c);
5 a:= d.a + e.a;
6 print „a=“+a;
7 d.a = a;
8 e.a = b;
9 print „sum=“+d.a;
Für die Variablen a, b und c wird angenommen, dass es sich um Variablen vom Typ Integer handelt. Wir setzen voraus, dass der Typ „Integer“ ein „Value-Type“ (Werttyp) ist. Darüber hinaus nehmen wir an, dass die Variablen d und e vom Typ „RefTy“ sind. Weiterhin soll gelten, dass „RefTy“ ein „Reference-Type“ (Referenztyp) ist.
2.2 Daten
In einem ersten Schritt sollen zunächst Datenquellen erkannt und markiert werden auf deren Grundlage anschliessend die Abhängigkeitsanalyse durchgeführt werden wird. Diese Daten repräsentieren bestimmte „Orte im Speicher“. Die Daten welche markiert werden, müssen aber nicht unbedingt exakt mit der Situation übereinstimmen, welche zur Laufzeit tatsächlich bestehen wird. Die Unterteilung basiert lediglich auf einer Analyse des Quellcodes und ist daher spekulativ. Aus diesem Grund werden die markieren Datenquellen in diesem Dokument als „abstract locations“ („abstrakte Speicherpositionen“) bezeichnet. Eine abstract location bezeichnet eine Menge von tatsächlichen Speicherpositionen, welche aber möglicherweise zur Laufzeit Aliase voneinander sein könnten und deshalb auf das Selbe Datum verweisen könnten.
Beispiel:
abstract locations sind markiert
0 A:=B+C;
1 if (A==1) {
2 B:=B+1; };
3 RefTy D := new RefTy(A,B);
4 RefTy D := new RefTy(B,C);
5 A:= D + D;
6 print „a=“+A;
7 D = A;
8 D = B;
9 print „sum=“+D;
Aus mathematischer Sicht stellt das Markieren der abstract locations eine Zerlegung in Äquivalenzklassen dar. Die in diesem Beispiel erzeugte Zerlegung lautet:
A= { a }
B = { b }
C = { c }
D = { d.a, e.a }
Es wird gefordert, dass alle
verschiedenen abstract locations zur Laufzeit garantiert keine Aliase
voneinander sein können. Alle Elemente, welche zur selben abstract location
gehören, können Aliase voneinander sein – müssen aber nicht. Ziel der Markierung
der abstract locations ist es daher, möglichst viele verschiedene abstract
locations zu markieren ohne die Forderung nach Korrektheit zu verletzen. Die
optimale Lösung kann nicht in linearer Zeit gefunden werden. Daher ist es
erforderlich einen sinnvolle Kompromiss zu finden, welcher ein möglichst gutes
Ergebnis liefert und gleichzeitig ein möglichst günstiges Zeitverhalten bietet.
Dieses Ziel zu erreichen ist je nach Programmiersprache und dem zu
analysierenden Quellcode unterschiedlich kompliziert. Weil Werttypen keine
Aliase besitzen können, kann zum Beispiel für Variablen welche Werttypen
aufnehmen angenommen werden, dass für jeden Identifier genau 1 abstract location
existiert. Komplizierter ist dies jedoch bei Referenztypen.
Hier muss eine Aliasanalyse durchgeführt werden um zu entscheiden, welche Identifier möglicherweise Aliase voneinander sein könnten. Für eine Aliasanalyse gibt es mehrere verschiedene Verfahren, welche unterschiedliches Zeitverhalten haben und unterschiedlich exakte Ergebnisse liefern können.
Als Beispiel für eine sehr einfache
Aliasanalyse könnte man annehmen, dass alle gleichnamigen Komponenten
von Objekten, welche zur gleichen Klasse gehören, möglicherweise Aliase
voneinander sein könnten und diese deshalb in einer gemeinsamen abstract
location zusammenfassen. So wie dies im obigen Beispiel mit „d.a“ und „e.a“
geschehen ist, wobei beide Objekte „d“ und „e“ zur Klasse „RefTy“
gehören.
Angenommen, dass die Klasse „RefTy“ die Komponenten „RefTy.a“ und „RefTy.b“
definiert. Vorausgesetzt, dass die Komponenten „a“ und „b“ Werttypen
sind, dann folgt daraus, dass die Komponenten „d.a“ und „e.b“ keine
Aliase voneinander sein können, obwohl „d“ und „e“ beide von der Klasse
„RefTy“ sind. Dies ist darin begründet, dass die Komponenten „a“ und „b“
Werttypen sind und deshalb keine Aliase besitzen können. Auch dann
nicht, wenn es sich bei den Objekten „d“ und „e“ um Aliase handeln
sollte, sind die Komponenten „a“ und „b“ dennoch verschieden.
Angenommen, dass die Komponenten „RefTy.a“ und „RefTy.b“ ihrerseits
ebenfalls Referenztypen sind, dann wird die Aliasanalyse nun rekursiv
auf diese Objekte und deren Komponenten angewendet. Sollten beide
Objekte „RefTy.a“ und „RefTy.b“ vom gleichen Typ sein, können diese
Aliase voneinander bilden, ansonsten nicht. Dieser Prozess ist nun
wiederum anwendbar auf Komponenten von „RefTy.a“ und „RefTy.b“ zum
Beispiel auf 2 Komponenten „RefTy.a.x“ und „RefTy.b.y“.
Ein weiteres Beispiel: Angenommen es gäbe ein Objekt „f“ vom Typ
„RefTy2“ und ein Objekt „g“ vom Typ „RefTy3“ so kann angenommen werden,
dass „f“ und „g“ zu verschiedenen abstract locations gehören, weil ihre
Basisklassen unterschiedlich sind und diese Objekte daher keine Aliase
voneinander sein können, obwohl „f“ und „g“ beides Referenztypen sind.
Zusätzlich zu den bereits genannten abstract locations kann es noch weitere geben, welche überhaupt keinem Ort im Speicher zur Laufzeit entsprechen müssen. Solche können eingeführt werden um das Ergebnis der Analyse insgesamt zu verbessern, oder aber sie werden wegen bestimmten Eigenschaften der Programmsprache notwendig. Zum Beispiel könnten Nullpointerchecks oder andere Anweisungen welche zur Laufzeit möglicherweise Ausnahmen erzeugen könnten ebenfalls abstract locations belegen. Diese Checks müssen weder explizit im Quellcode auftauchen, noch ist es notwendig, dass zur Laufzeit tatsächlich jemals Speicher dafür allokiert wird. Aus Gründen des besseren Verständnis wurde im oben beschriebenen Beispiel jedoch darauf verzichtet solche abstract locations einzuführen.
2.3 Operatoren
Nachfolgend muss für alle abstract locations geprüft werden, welche Anweisungen Lese- oder Schreibzugriffe auf diesen Speicherorten ausführen. Als Ergebnis wird eine Tabelle erstellt, welche jeder Anweisung des Beispielcodes jeweils eine Menge von Lesezugriffen und eine Menge von Schreibzugriffen zuordnet.
Lesezugriffe werden dabei mit „use“ und Schreibzugriffe mit „def“ für „definition“ bezeichnet.
0 def A; use B,C
1 use A
2 def B; use B
3 def D; use A,B
4 def D; use B,C
5 def A; use D
6 use A
7 def D; use A
8 def D; use B
9 use D
2.4 Abhängigkeitsanalyse
Für die Abhängigkeitsanalyse ist es notwendig zu entscheiden, für welches Modell man Datenabhängigkeiten aufzeigen möchte. Dies ist deshalb wichtig, weil von dieser Entscheidung abhängt, welche Datenabhängigkeiten aufgezeichnet werden und auf welche verzichtet werden kann. In diesem Beispiel wird das CREW-Modell zugrunde gelegt. CREW steht für „concurrent read, exclusiv write“. Diese bedeutet, dass für Lesezugriffe auf die gleiche Position im Speicher angenommen wird, dass diese konkurrierend und somit unabhängig voneinander geschehen können. Für Schreibzugriffe wird hingegen angenommen, dass diese exklusiv erfolgen müssen, also Schreibzugriffe abhängig voneinander auftreten.
Es gibt 4 Typen von Abhängigkeiten, welche auftreten können:
- def -> use echte Abhängigkeit
(„TRUE dependency“) - use -> def umgekehrte Abhängigkeit
(„ANTI dependency“) - def -> def Ausgabeabhängigkeit
(„OUTPUT dependency“) - use -> use Eingabeabhängigkeit
(„INPUT dependency“)
Auf die Abhängigkeit 4. kann in dieser Betrachtung verzichtet werden, weil das CREW-Modell angewendet wird. Dabei spielt die bei 4. genannte Abhängigkeit keine Rolle.
Die Abhängigkeiten sind in folgender Weise zu lesen: „def -> use“
bezeichnet den Fall, dass ein Lesezugriff auf eine abstract location
stattfindet, nachdem ein Schreibzugriff auf die gleiche abstract
location stattgefunden hat. Dies ist eine wichtige Abhängigkeit weil sie
aussagt, dass der Lesezugriff auf diese abstract location nicht
stattfinden darf, bevor der Schreibzugriff abgeschlossen ist, weil
ansonsten möglicherweise ein ungültigtes Datum gelesen wird.
Die „ANTI dependency“ („use -> def“) bezeichnet den Fall, dass ein
Schreibzugriff auf eine abstract location stattfindet, nachdem
Lesezugriff auf die gleiche abstract location stattgefunden hat. Dies
bedeutet, dass der Schreibzugriff warten muss, bis der Lesezugriff
stattgefunden hat, weil sonst das Ergebnis für den Lesezugriff unültig
werden würde.
Mit „def -> def“ wird der Fall bezeichnet, dass zwei Schreibzugriffe auf
die gleiche abstract location nacheinander stattfinden. Diese ist
deshalb wichtig zu markieren, weil dadurch angezeigt wird, dass der
zweite Schreibzugriff nicht stattfinden darf, bevor der erste
abgeschlossen wurde. Sonst besteht die Gefahr, dass der erste
Schreibzugriff das Datum des Schreibzugriffes, der eigentlich später im
Programmablauf folgt, überschreibt und dadurch das Datum ungültig wird.
2.4.1 Ablauf der Abhängigkeitsanalyse
Die Analyse findet in 2 Schritten statt. Zuerst werden die Anweisungen in aufsteigender Reihenfolge (von oben nach unten) durchlaufen um TRUE- und OUTPUT- dependencies zu finden. Anschliessend werden im 2. Schritt die Anweisungen ein zweites Mal in absteigender Reihenfolge (von unten nach oben) durchlaufen, um ANTI dependencies zu finden.
Dabei wird wie folgt vorgegangen:
1. Schritt – durchlaufe alle Anweisungen in aufsteigender Reihenfolge
betrachte die „def“s in Anweisung „i“ { Wenn es für eine abstract location ein anderes „def“ gibt, dass vor der Anweisung „i“ auftaucht dann zeichne zu dieser Anweisung eine OUTPUT dependency ein. } betrachte alle „use“s in Anweisung „i“ { Wenn es für eine abstract location ein „def“ gibt, dass vor der Anweisung „i“ auftaucht dann zeichne zu dieser Anweisung eine TRUE dependency ein. }
2. Schritt – durchlaufe alle Anweisungen in absteigender Reihenfolge
betrachte alle „use“s in Anweisung „i“ { Wenn es für eine abstract location ein „def“ gibt, dass vor der Anweisung „i“ auftaucht dann zeichne zu dieser Anweisung eine ANTI dependency ein. }
Es bietet sich an, beim Durchlaufen der Anweisungen für jede abstract location eine Liste der „def“s und „use“s zu verwalten, das diese im Verlauf des Verfahrens häufig gebraucht werden.
2.4.2 Anwendung auf das Beispielprogramm
Schritt 1: Einträge „vorwärts“ durchlaufen
DEF = []
Betrachte
Zeile 0: def A; use B,C
- keine Abhängigkeiten, weil 1. Anweisung
aktualisiere die
Liste...
DEF = [A=>0]
Betrachte
Zeile 1: use A
- TRUE Abhängigkeit zu Zeile 0 für abstract location A
aktualisiere die
Liste...
DEF = [A=>0]
Betrachte
Zeile 2: def B; use B
- keine Abhängigkeit gefunden
aktualisiere die
Liste...
DEF = [A=>0,B=>2]
Betrachte
Zeile 3: def D; use A,B
- TRUE Abhängigkeit zu Zeile 0 für abstract location A
- TRUE Abhängigkeit zu Zeile 2 für abstract location B
aktualisiere die
Liste...
DEF = [A=>0,B=>2,D=>3]
Betrachte
Zeile 4: def D; use B,C
- OUTPUT Abhängigkeit zu Zeile 3 für abstract location D
- TRUE Abhängigkeit zu Zeile 2 für abstract location B
aktualisiere die
Liste...
DEF = [A=>0,B=>2,D=>4]
Betrachte
Zeile 5: def A; use D
- OUTPUT Abhängigkeit zu Zeile 0 für abstract location A
- TRUE Abhängigkeit zu Zeile 4 für abstract location D
aktualisiere die
Liste...
DEF = [A=>5,B=>2,D=>4]
Betrachte
Zeile 6: use A
- TRUE Abhängigkeit zu Zeile 5 für abstract location A
aktualisiere die
Liste...
DEF = [A=>5,B=>2,D=>4]
Betrachte
Zeile 7: def D; use A
- OUTPUT Abhängigkeit zu Zeile 4 für abstract location D
- TRUE Abhängigkeit zu Zeile 5 für abstract location A
aktualisiere die
Liste...
DEF = [A=>5,B=>2,D=>7]
Betrachte
Zeile 8: def D; use B
- OUTPUT Abhängigkeit zu Zeile 7 für abstract location D
- TRUE Abhängigkeit zu Zeile 2 für abstract location B
aktualisiere die
Liste...
DEF = [A=>5,B=>2,D=>8]
Betrachte Zeile 9: use D
- TRUE Abhängigkeit zu Zeile 8 für abstract location D
Ende Schritt 1.
Das gleiche nun noch einmal „rückwärts“ in Schritt 2:
DEF = []
Betrachte Zeile 9: use D
- keine Abhängigkeiten, weil 1. Anweisung
aktualisiere die Liste...
DEF = []
Betrachte Zeile 8: def D; use B
- keine Abhängigkeit gefunden
aktualisiere die Liste...
DEF = [D=>8]
Betrachte Zeile 7: def D; use A
- keine Abhängigkeit gefunden
aktualisiere die Liste...
DEF = [D=>7]
Betrachte Zeile 6: use A
- keine Abhängigkeit gefunden
aktualisiere die Liste...
DEF = [D=>7]
Betrachte Zeile 5: def A; use
D
- ANTI Abhängigkeit zu Zeile
7 für abstract location D
aktualisiere die Liste...
DEF = [A=>5,D=>7]
Betrachte Zeile 4: def D; use B,C
- keine Abhängigkeit gefunden
aktualisiere die Liste...
DEF = [A=>5,D=>4]
Betrachte Zeile 3: def D; use A,B
- ANTI Abhängigkeit zu Zeile 5 für abstract location A
aktualisiere die Liste...
DEF = [A=>5,D=>5]
Betrachte Zeile 2: def B; use B
- keine Abhängigkeit gefunden
aktualisiere die Liste...
DEF = [A=>5,B=>2,D=>7]
Betrachte Zeile 1: use A
- ANTI Abhängigkeit zu Zeile 5 für abstract location A
aktualisiere die Liste...
DEF = [A=>5,B=>2,D=>7]
Betrachte Zeile 0: def A; use B,C
- ANTI Abhängigkeit zu Zeile 2 für
abstract location B
Ende Schritt 2.
Damit ist der zweite Schritt abgeschlossen. Aufgegliedert nach den abstract locations ergeben sich die in Abbildung 1 dargestellten Abhängigkeiten für die abstract locations A, B und D.
Für die abstract location C haben sich keine Abhängigkeiten ergeben, weil kein Schreibzugriff auf diese Variable im Beispielcode aufgetreten ist.
Dies ergibt folgende graphische Darstellung:

Abbildung 1
Legende:

2.5 Abhängigkeitsgraph
|
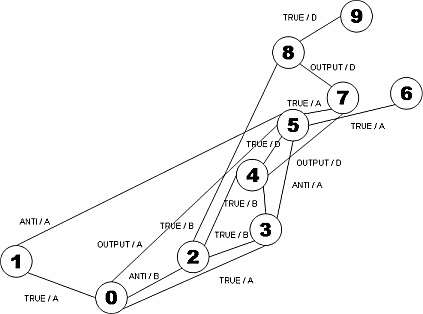
Die in Abbildung 1 als Graphen erfassten Abhängigkeiten lassen sich zusammenfassen und in einem Abhängigkeitsgraphen darstellen. Den Abhängigkeitsgraph, welcher sich dabei ergibt zeigt Abbildung 2.
Aus Abbildung 2 lässt sich entnehmen, zwischen welchen Anweisungen des Beispiels Abhängigkeiten bestehen und welche Anweisungen unabhängig sind. Die Kanten sind dabei gemäss der Reihenfolge der Anweisungen 0-9 von unten nach oben gerichtet. Unter anderem ist daraus erkennbar, dass eine Kante zwischen Anweisung 8 und Anweisung 2 besteht. Damit sind Anweisung 8 und 2 „direkt abhängig“. Die direkte Abhängigkeitsbeziehung wird durch die gemeinsame Kante, welche beide Knoten verbindet, zum Ausdruck gebracht. Anweisung 8 und Anweisung 5 sind „indirekt abhängig“ voneinander. Es besteht zwar keine direkte Kante zwischen Knoten 5 und Knoten 8, aber beide Knoten besitzen eine Kante zu Knoten 7. Daher sind beide Anweisungen über die Anweisung 7 indirekt abhängig. Darüber hinaus lässt sich ablesen, dass zum Beispiel Anweisung 6 und Anweisung 7 unabhängig sind. Es besteht keine Kante zwischen beiden Knoten. Zwar haben Knoten 6 und Knoten 7 beide eine Kante zu Knoten 5 und sind damit direkt von Anweisung 5 abhängig. Aber wegen der Lesrichtung des Graphen von unten nach oben sind die Anweisungen 6 und 7 voneinander dennoch unabhängig.
Die Kanten des Abhängigkeitsgraphen können zusätzlich mit den jeweiligen Abhängigkeiten und der Bezeichnung der abstract location beschriftet werden, auf welche sich die Kante bezieht. Darauf wurde zugunsten einer besseren Übersicht in Abbildung 2 jedoch verzichtet. Zum Zweck der Vollständigkeit zeigt Abbildung 3 den Abhängigkeitsgraphen inklusive Kantenbenennung. |
3. Algorithmus
|
Im Folgenden Abschnitt 3 wird das in Abschnitt 2.4.1 vorgestellte und in Abschnitt 2.4.2 an im Beispiel demonstrierte Verfahren in einen konkreten (Pseudocode) Algorithmus überführt. Abschließend werden Überlegungen zur Komplexität des so gewonnenen Algorithmus angestellt. |
3.1 Entwurf eines Algorithmus
Wie bereits erwähnt kann es für das Auffinden von abstract locations mehrere Verfahren geben. Zusätzlich wird ein weiteres Verfahren benötigt, welches die Anweisungen des eingegebenen Programmfragments überführt in eine Tabelle von Lese- und Schreibzugriffen auf den gefundenen abstract locations. In diesem Abschnitt nehmen wir zunächst an, dass diese beiden Verfahren bereits gegeben sind. Stattdessen beschränken wir uns zunächst auf den eigentlichen Arbeitsschritt: das Auffinden von Abhängigkeiten innerhalb eines gegebenen Programmblocks.
Vergleichen sie dazu den folgenden Algorithmus mit dem in Abschnitt 2.4.1 beschriebenen Verfahren.
Dabei wird vorausgesetzt, dass als Eingabe eine korrekte Unterteilung in abstract locations existiert und eine korrekte Tabelle der Lese- und Schreibzugriffe vorliegt.
Eingabe:
- eine sortierte Liste aller Anweisungen (instructions)
- zu jeder Anweisung „p“ jeweils Listen der „use“s und „def“s
- „use“s bzw. „def“s sind Listen der abstract locations, auf denen die Anweisung „p“ Lese- bzw. Schreibzugriffe durchführt
Beispiel:
instruction[0] = { use = [A,B] , def = [C] };
instruction[1] = { use = [ ] , def = [A] };
...
instruction[n] = { use = [C] , def = [ ] };
Ausgabe:
Eine Liste der gefundenen Abhängigkeiten
Algorithmus
1. Schritt – durchlaufe alle Anweisungen in aufsteigender Reihenfolge, um TRUE – und OUTPUT – Abhängigkeiten zu finden
DEF = [list of last encounterd „def“s on abstract locations] ForEach (instruction „p“ in forward order) { ForEach (use of abstract location „aloc“ in „p“) { IF (DEF[„aloc“] is not empty) { create TRUE dependency (DEF[„aloc“],p) } } ForEach (def of abstract location „aloc“ in „p“) { IF (DEF[„aloc“] is not empty) { create OUTPUT dependency (DEF[„aloc“],p) } DEF[„aloc“] := p } }
2. Schritt – durchlaufe alle Anweisungen in absteigender Reihenfolge, um ANTI – Abhängigkeiten zu finden
DEF = [list of last encountered „def“s on abstract locations] ForEach (instruction „p“ in backward order) { ForEach (def of abstract location „aloc“ in „p“) { DEF[„aloc“] := p } ForEach (use of abstract location „aloc“ in „p“) { IF (DEF[„aloc“] is not empty) { create ANTI dependency(p,DEF[„aloc“]) } }
Der Pseudocode entspricht inhaltlich dem Algorithmus in: Chambers, Pechtchanski, Sarkar, Serrano, Srinivasan. Dependency Analysis for Java. IBM.
Die grundlegende Idee dieses Algorithmus besteht darin, eine Liste der zuletzt angetroffenen defintions (also der Schreibzugriffe) für jede abstract location zu verwalten. Während die Liste der Anweisungen durchlaufen wird, wird diese Liste ständig aktualisiert. Wird für in Anweisung „i“ ein Schreibzugriff für eine abstract location „a“ gefunden, so wird gesetzt: DEF[a] := i. Falls in einer späteren Anweisung erneut ein Schreibzugriff auf die gleiche abstract location festgestellt wird, so wird der alte Wert für DEF[a] überschrieben.
Der Algorithmus durchläuft folglich zunächst „vorwärts“ die
Liste der Anweisungen.
Dabei vergleicht dieser für jede Anweisung „p“ die Liste der abstract locations
auf welche die Anweisung „p“ Lesezugriffe durchführt mit der Liste „DEF“ der
zuvor erkannten Schreibzugriffe. Gibt es eine abstract location „a“, welche in
beiden Listen auftaucht, so ist dies gleichbedeutend damit, dass „a“ zuvor
geschrieben und in Anweisung „p“ gelesen wird (def->use). Demnach wird eine
TRUE-Abhängigkeit erzeugt. Diese Abhängigkeit besteht zwischen der schreibenden
Anweisung und Anweisung „p“ welche die abstract location „a“ liest. Also:
zwischen den Anweisungen „DEF[a]“ und „p“.
Außerdem wird die Liste der Schreibzugriffe in Anweisung „p“ ebenfalls mit der
Liste der zuvor erkannten Schreibzugriffe verglichen. Gibt es eine abstract
location „b“ welche in beiden Listen auftaucht, so ist dies gleichbedeutend
damit, dass „b“ zuvor geschrieben und ihr Wert nun in Anweisung „p“ erneut
überschrieben wird (def->def). Folglich wird eine OUTPUT-Abhängigkeit zwischen
den Anweisungen „DEF[b]“ und „p“ erzeugt. Während des Durchlaufens der
Anweisungen wird die Liste „DEF“ in jedem Schritt aktualisiert.
Dies geschieht wird realisiert durch die Anweisung: DEF[„aloc“] := p
Im 2. Schritt wird die Liste der Anweisungen „rückwärts“ durchlaufen um ANTI-Abhängigkeiten zu finden. Dies ist notwendig, weil mit der Liste „DEF“ lediglich eine Liste der Schreibzugriffe existiert. Im 1. Schritt können daher nur Abhängigkeiten der Form „def->xxx“ gefunden werden, weil keine Informationen über bereits durchgeführte Lesezugriffe gespeichert werden. Der 2. Schritt ist daher notwendig um Abhängigkeiten der Form „xxx->def“ zu finden. Die Vorgehensweise beim Auffinden von ANTI-Abhängigkeiten ist darüber hinaus analog zu Schritt 1.
Es wäre jedoch ebenfalls denkbar, zusätzlich zur Liste „DEF“ der Schreibzugriffe eine Liste „USE“ der Lesezugriffe zu verwalten und dadurch den 2. Schritt zu sparen. Ob dies tatsächlich sinnvoll ist, müsste jedoch im Einzelfall geprüft werden.
Durch zusammenfassen der Schritte 1 und 2 ergibt sich der folgende, vereinfachte Algorithmus.
DEF = [list of last encounterd „def“s on abstract locations] USE = [list of last encounterd „use“s on abstract locations] ForEach (instruction „p“ in forward order) { ForEach (use of abstract location „aloc“ in „p“) { IF (DEF[„aloc“] is not empty) { create TRUE dependency (DEF[„aloc“],p) } USE[„aloc“] := p } ForEach (def of abstract location „aloc“ in „p“) { IF (DEF[„aloc“] is not empty) { create OUTPUT dependency (DEF[„aloc“],p) } IF (USE[„aloc“] is not empty) { create ANTI dependency (USE[„aloc“],p) } DEF[„aloc“] := p } }
Obwohl diese Form des Algorithmus kürzer gemessen an der Zahl der Anweisungen ist, ist sie dennoch ungünstiger im Speicherverhalten. Dies ergibt sich aus der Tatsache, dass zusätzlich eine Liste „USE“ der Lesezugriffe verwaltet werden muss. Zwar hat sich die Zahl der Vergleichsoperation verringert, allerdings wurde gleichzeitig die Zahl der Speicherzugriffe (dabei insbesondere der Schreibzugriffe) erhöht. Unter der Annahme, dass ein Zugriff auf den Hauptspeicher in heutigen Personal-Computern in der Regel eine relativ größere Zeitspanne in Anspruch nimmt als das Durchführen einer Vergleichsoperation ist daher zu erwarten, dass diese Variante des Algorithmus wahrscheinlich eine ungünstigere Performance aufweisen wird. Obwohl dies möglicherweise dem ersten subjektiven Eindruck widerspricht, welcher sich aus einer oberflächlichen, subjektiven Betrachtung des Pseudocodes ergibt. Im Folgenden wird daher weiterhin die ursprüngliche Variante des Algorithmus besprochen.
Wie bereits in Abschnitt 1 erwähnt wird von diesem Algorithmus gefordert, dass alle Anweisungen, zwischen denen tatsächlich eine Abhängigkeitsbeziehung besteht, durch den Algorithmus gefunden werden müssen. Es wäre folglich zu zeigen, dass es keine Abhängigkeit geben kann, welche vom Algorithmus nicht erkannt wird.
Zu diesem Zweck ist es erforderlich eine Voraussetzung zu treffen, dass alle Eingaben welche der Algorithmus erhält bereits korrekt sind. Dies betrifft folglich insbesondere die abstract locations und die Liste der Lese- und Schreibzugriffe.
Es gibt 3 Fälle in denen eine Abhängigkeit für eine abstract location „a“ auftreten kann:
- def(a) vor use(a) (TRUE)
- def(a) vor def(a) (OUTPUT)
- use(a) vor def(a) (ANTI)
Im Folgenden wird gezeigt, dass es in keinem der 3 Fälle eine abstract location „a“ geben kann, für welche der Algorithmus die Abhängigkeit nicht feststellt.
Angenommen „a“ seine TRUE-Abhängigkeit zwischen den Anweisungen „i“ und „k“, mit i<k:
Es folgt aus:
ForEach (instruction „p“ in forward order)
dass der Algorithmus alle Anweisungen bearbeitet. Also insbesondere auch die
Anweisungen „i“ und „k“. Aus i<k und der Abarbeitung der Anweisungen in
aufsteigender Reihenfolge durch den Algorithmus folgt, dass der Algorithmus die
Anweisung „i“ vor der Anweisung „k“ bearbeitet.
Aus der Voraussetzung, dass die Eingaben korrekt sind, ergibt sich, dass die Anweisung DEF[„aloc“] := p den Schreibzugriff auf die abstract location „a“ in der Anweisung „i“ vermerkt und es folgt ebenfalls daraus, dass der Lesezugriff auf die abstract location „a“ in der Anweisung „k“ erkannt wird.
- Fall: zum Zeitpunkt der Bearbeitung der Anweisung „k“
gilt „DEF[a] == i“.
Weil der Lesezugriff auf „a“ wie beschrieben erkannt wird und „DEF[a]“ aufgrund der Belegung „DEF[a]=i“ nicht leer ist, wird die Zeile create TRUE dependency (DEF[„aloc“],p) ausgeführt und somit eine TRUE-Abhängigkeit zwischen der Anweisung „i“ und der Anweisung „k“ erzeugt.
KORREKT. - Fall: zum Zeitpunkt der Bearbeitung der Anweisung „k“
gilt „DEF[a] != i“.
Dann gilt 1) „DEF[a]“ ist nicht leer und 2) „DEF[a]=x“ mit k<x<i
Es wird folglich eine TRUE-Abhängigkeit zwischen der Anweisung „i“ und der Anweisung „x“ erzeugt.
Es gilt außerdem:
es gibt eine Folge von Anweisungen „y[0],y[1]...y[n]“ mit k<y[z]<x, 0<=z<=n für die gilt: 1) es besteht eine Abhängigkeitsbeziehung zwischen den Anweisungen y[0] und k, 2) es besteht eine Abhängigkeitsbeziehung zwischen den Anweisungen y[n] und x, 3) für alle Anweisungen y[z] mit 0<z<=n gilt: es besteht eine Abhängigkeitsbeziehung zwischen den Anweisungen y[z] und y[z-1].
Daraus folgt: es besteht mittelbar über die Folge von Anweisungen „y[0],y[1]...y[n]“ eine (indirekte) Abhängigkeitsbeziehung zwischen den Anweisungen „i“ und „k“.
KORREKT.
Der Beweis erfolgt für die Fälle analog.
Entscheidend für die Komplexität des Algorithmus ist die Tatsache, dass der Algorithmus transitive Abhängigkeitsbeziehungen ignoriert. Eine transitive Abhängigkeitsbeziehung besteht zum Beispiel wenn gilt: a>b>c und a>c. Die transitive Beziehung a>c ergibt sich logisch aus der Beziehung a>b>c und wird vom Algorithmus ignoriert. Diese Eigenschaft ergibt sich dadurch, dass der Algorithmus für jede abstract location lediglich den zuletzt angetroffenen Schreibzugriff speichert und dabei Informationen über frühere Speicherzugriffe ersetzt.
Aufgrund dieser Eigenschaft des Algorithmus wird auch die Zahl der erforderlichen Vergleichsoperationen verringert. Die Zahl der in der Liste „DEF“ gespeicherten Anweisungen übersteigt somit nie die Anzahl der abstract locations. Zum Vergleich: ohne diese Eigenschaft würde die Liste „DEF“ für einen Block mit n Anweisungen und m abstract locations bis zu n*m Anweisungen enthalten. Dadurch ergäbe sich im schlechtesten Fall ein Ergebnis von mindestens O(n2) für diesen Algorithmus.
Durch die Einschränkung ergibt sich jedoch eine wesentlich geringere Anzahl an gespeicherten Anweisungen und somit auch eine geringere Zahl an Vergleichsoperationen.
ForEach (use of abstract location „aloc“ in „p“) { IF (DEF[„aloc“] is not empty) { create ANTI dependency (p,DEF[„aloc“]) } }
Aufgrund der benannten Eigenschaft des Algorithmus kann man annehmen, dass die Liste „DEF“ eine quasi-konstante Anzahl von Einträgen enthält. Es ergibt sich daher für dieses Codefragment eine Komplexität von O(c), wobei „c“ als konstant angenommen werden kann. Daher folgt die Annahme, dass die Komplexität des gesamten Blocks O(1) beträgt.
Insgesamt ergibt sich somit angewendet auf den gesamten Algorithmus eine Komplexität von O(2*n), wie in Abbildung 4 verdeutlicht. Es handelt sich demnach um einen Algorithmus mit linearer Komplexität.

Allerdings muss für die Betrachtung der Komplexität des gesamten Verfahrens auch das Auffinden der abstract locations und die Unterteilung in Lese- und Schreibzugriffe berücksichtigt werden. Somit insbesondere auch der Aliasanalyse. In Verbindung mit diesen Verfahren ist es möglich, dass sich eine nicht-lineare Komplexität für das Verfahren insgesamt ergibt.
(ac/tom) Diskussion
Diskussion